Thurstone L L a Law of Comparative Judgment Psychological Review Vol 34 Pp 273-286 1927

A Police of Comparative Judgment

Louis L. Thurstone
University of Chicago

The object of this newspaper is to describe a new psycho-physical law which may be called the police force of comparative judgment and to show some of its special applications in the ,measurement of psychological values. The police of comparative judgment is implied in Weber's law and in Fechner'southward police force. The law of comparative judgment is applicable non simply to the comparison of physical stimulus intensities simply also to qualitative comparative judgments such as those of excellence of specimens in an educational scale and it has been applied in the measurement of such psychological values as a serial of opinions on disputed public issues. The latter application of the police force will be illustrated in a forthcoming written report. It should be possible also to verify information technology on comparative judgments which involve simultaneous and successive dissimilarity.

The police has been derived in a previous article and the present study is mainly a description of some of its applications. Since several new concepts are involved in the formulation of the law information technology has been necessary to invent several terms to draw them, and these volition be repeated here.

Let us suppose that we are confronted with a series of stimuli or specimens such equally a series of grayness values, cylindrical weights, handwriting specimens, children'due south drawings, or any other series of stimuli that are field of study to comparison. The first requirement is of course a specification equally to what it is_, that nosotros are to judge or compare. Information technology may be gray values, or weights, or excellence, or whatsoever other quantitative or qualitative attribute most which we tin think `more' or `less' for each specimen. This attribute which may be assigned, equally it were, in differing amounts to each specimen defines what nosotros shall call the psychological continuum for that particular project in measurement.

---

( 274)

Every bit nosotros inspect 2 or more than specimens for the task of comparison there must exist some kind of procedure in us by which we react differently to the several specimens, by which nosotros place the several degrees of excellence or weight or grayness value in the specimens. Y'all may adapt your own predilections in calling this procedure psychical, neural, chemical, or electrical only it will be called here in a non-committal mode the discriminal process because its ultimate nature does non concern the formulation of the police of comparative judgment. If then, one handwriting specimen seems to be more splendid than a 2d specimen, then the 2 discriminal processes of the observer are different, at to the lowest degree on this occasion.

The so-chosen `just noticeable departure' is contingent on the fact that an observer is not consistent in his comparative judgments from one occasion to the next. He gives different comparative judgments on successive occasions about the same pair of stimuli. Hence we conclude that the discriminal procedure respective to a given stimulus is not fixed. Information technology fluctuates. For whatsoever handwriting specimen, for example, there is 1 discriminal procedure that is experienced more often with that specimen than other processes which correspond to higher or lower degrees of excellence. This most common procedure is called here the modal discriminal process for the given stimulus.

The psychological continuum or scale is and then constructed or defined that the frequencies of the respective discriminal processes for whatsoever given stimulus form a normal distribution on the psychological scale. This involves no supposition of a normal distribution or of anything else. The psychological calibration is at best an artificial construct. If it has whatsoever concrete reality we certainly accept not the remotest idea what it may be like. We exercise not assume, therefore, that the distribution of discriminal processes is normal on the scale considering that would imply that the calibration is there already. We define the scale in terms of the frequencies of the discriminal processes for any stimulus. This artificial construct, the psychological calibration, is and then spaced off that the frequencies of the discriminal processes for any given stimulus form a normal distribution

---

( 275) on the calibration. The separation on the scale betwixt the discriminal process for a given stimulus on any particular occasion and the modal discriminal process for that stimulus we shall call the discriminal departure on that occasion. If on a detail occasion, the observer perceives more than the usual degree of excellence or weight in the specimen in question, the discriminal departure is at that instant positive. In a similar way the discriminal departure at some other moment volition be negative.

The standard deviation of the distribution of discriminal processes on the calibration for a item specimen will be called its discriminal dispersion.

This is the cardinal concept in the present analysis. An cryptic stimulus which is observed at widely different degrees of excellence or weight or gray value on unlike occasions will have of course a large discriminal dispersion. Some other stimulus or specimen which is provocative of relatively slight fluctuations in discriminal processes volition accept, r similarly, a minor discriminal dispersion.

The scale difference betwixt the discriminal processes of two specimens which are involved in the aforementioned judgment will be called the discriminal difference on that occasion. If the two stimuli exist denoted A and B and if the discriminal processes corresponding to them be denoted a and b on whatever i occasion, and so the discriminal difference will be the calibration distance (a — b) which varies of course on different occasions. If, in i of the comparative judgments, A seems to be better than B, then, on that occasion, the discriminal difference (a — b) is positive. If, on some other occasion, the stimulus B seems to be the better, so on that occasion the discriminal divergence (a — b) is negative.

Finally, the calibration altitude between the modal discriminal processes for any two specimens is the separation which is assigned to the two specimens on the psychological scale. The two specimens are so allocated on the scale that their separation is equal to the separation between their corresponding modal discriminal processes.

We tin now state the law of comparative judgment as follows:

---

( 176)

in which

S_i and S ₂ are the psychological scale values of the two compared stimuli.

x₁₂ = the sigma value corresponding to the proportion of judgments p_1>ii. When p_ane>2 is greater than .50 the numerical value of x ₁₂ is positive. When p_1>2 is less than .50 the numerical value of x₁₂ is negative.

σ_one = discriminal dispersion of stimulus R_l.

σ_two = discriminal dispersion of stimulus R_ii

r = correlation between the discriminal deviations of R _i and R_ii in the same judgment.

This law of comparative judgment is basic for all experimental piece of work on Weber's police force, Fechner's law, and for all educational and psychological scales in which comparative judgments are involved. Its derivation will not be repeated hither because information technology has been described in a previous article.[two] Information technology applies fundamentally to the judgments of a single observer who compares a series of stimuli past the method of paired comparison when no `equal' judgments are immune. It is a rational equation for the method of constant stimuli. It is assumed that the single observer compares each pair of stimuli a sufficient number of times so that a proportion, pa>a, may exist determined for each pair of stimuli.

For the practical application of the law of comparative judgment we shall consider five cases which differ, in assumptions, approximations, and degree of simplification. The more assumptions we care to brand, the simpler will be the observation equations. These five cases are as follows:

Case I.—The equation can exist used in its complete form for paired comparison information obtained from a single discipline when simply two judgments are allowed for each observation such as `heavier' or `lighter,' `better' or `worse,' etc. There will be ane observation equation for every observed proportion of judgments. Information technology would be written, in its consummate form, thus:

< insert formula 1 >

---

( 177)

According to this equation every pair of stimuli presents the possibility of a unlike correlation between the discriminal deviations. If this caste of freedom is immune, the problem of psychological scaling would be insoluble because every observation equation would introduce a new unknown and the number of unknowns would then always be greater than the number of observation equations. In lodge to make the problem soluble, it is necessary to make at least 1 assumption, namely that the correlation between discriminal deviations is practically constant throughout the stimulus series and for the single observer. Then, if we take northward stimuli or specimens in the scale, we shall accept 2 n(north — I) observation equations when each specimen is compared with every other specimen. Each specimen has a scale value, S,, and a discriminal dispersion, a_l, to be determined. There are therefore 2n unknowns. The calibration value of one of the specimens is chosen as an origin and its discriminal dispersion as a unit of measurement, while r is an unknown which is assumed to be constant for the whole series. Hence, for a scale of n specimens at that place will be (2n — i) unknowns. The smallest number of specimens for which the trouble is soluble is five. For such a scale there volition be ix unknowns, four scale values, four discriminal dispersions, and r. For a calibration of five specimens there will be ten observation equations.

The statement of the constabulary of comparative judgment in the grade of equation I involves 1 theoretical assumption which is probably of modest importance. It assumes that all positive discriminal differences (a — b) are judged A > B, and that all negative discriminal differences (a — b) are judged A < B. This is probably not absolutely correct when the discriminal differences of either sign are very small. The assumption would not affect the experimentally observed proportion p A> a if the pocket-size positive discriminal differences occurred as often every bit the pocket-sized negative ones. As a matter of fact, when p A> a is greater than .50 the small positive discriminal differences (a — b) are slightly more than frequent than the negative perceived differences (a — b). Information technology is probable that rather refined experimental procedures are necessary to

---

( 178) isolate this consequence: The effect is ignored in our nowadays analysis.

Instance Two.—The law of comparative judgment as described nether Case I refers fundamentally to a series of judgments of a single observer. It does non constitute an assumption to say that the discriminal processes for a single observer give a normal frequency distribution on the psychological continuum. That is a part of the definition of the psychological scale. Simply it does constitute an assumption to take for granted that the various degrees of an attribute of a specimen perceived in it by a grouping of subjects is a normal distribution. For example, if a weight-cylinder is lifted by an observer several hundred times in comparison with other cylinders, it is possible to define or construct the psychological scale so that the distribution of the apparent weights of the cylinder for the single observer is normal. Information technology is probably safe to assume that the distribution of apparent weights for a group of subjects, each subject perceiving the weight only in one case, is besides normal on the aforementioned calibration. To transfer the reasoning in the aforementioned way from a single observer to a group of observers for specimens such as handwriting or English language Composition is not so certain. For practical purposes information technology may be assumed. that when a group of observers perceives a specimen of hand-writing, the distribution of excellence that they read into the specimen is normal on the psychological continuum of perceived excellence. At least this is a safety assumption if the group is not split up in some curious style with prejudices for or against detail elements of the specimen.

With the assumption just described, the law of comparative judgment, derived. for the method of abiding stimuli. with two responses, can exist extended to data collected from a grouping of judges in which each judge compares, each stimulus with every other stimulus just once. The other assumptions of Case I apply also to Case 2.

Case III.—Equation 1 is bad-mannered to handle equally an observation equation for a scale. with a large number of specimens. In fact the, arithmetical labor of constructing an educational or psychological scale with it is almost prohibitive. The

---

( 179) equation can be simplified if the correlation r tin exist assumed to be either zero or unity. It is a prophylactic supposition that when the stimulus series is very homogeneous with no distracting attributes, the correlation between discriminal deviations is low and perhaps even zero unless nosotros encounter the event of simultaneous or successive contrast. If we have the correlation every bit zero, we are really assuming that the degree of excellence which an observer perceives in 1 of the specimens has no influence on the caste of excellence that he perceives in the comparison specimen. There are 2 effects that may be operative here and which are antagonistic to each other.

(i) If you look at 2 handwriting specimens in a mood slightly more than generous and tolerant than commonly, you may perceive- a degree of excellence in specimen A a petty higher than its mean excellence. Only at the same moment specimen B is besides judged a piddling higher than its boilerplate or mean excellence for the same reason. To the extent that such a factor is at work the discriminal deviations will tend to vary together and the correlation r will be high and positive.

(ii) The opposite upshot is seen in simultaneous contrast. When the correlation between the discriminal deviations is negative the police of comparative judgment gives an exaggerated psychological divergence (S_l— South₂) which we know as simultaneous or successive dissimilarity. In this type of comparative judgment the discriminal deviations are negatively associated. It is likely that this outcome: tends to be a minimum when the specimens have other perceivable attributes, and that information technology is a maximum when other distracting stimulus differences are removed. If this statement should exist experimentally verified, it would found an interesting generalization in perception.

If our final generalization is correct, it should be a safe assumption to write r = 0 for those scales in which the specimens are rather complex such every bit handwriting specimens and childrens� drawings. If we look at two handwriting specimens and perceive one of them every bit unusually fine, information technology probably tends to depress somewhat the degree of excellence

---

( 180) we would unremarkably perceive in the comparison specimen, but this outcome is slight compared with the simultaneous contrast perceived in lifted weights and in gray values. Furthermore, the simultaneous contrast is slight with modest stimulus differences and it must exist recalled that psycho-logical scales are based on comparisons in the subliminal or barely supraliminal range.

The correlation between discriminal deviations is probably high when the two stimuli give simultaneous contrast and are quite far apart on the calibration. When the range for the correlation is reduced to a scale altitude comparable with the deviation limen, the correlation probably is reduced nearly to zero. At whatever rate, in guild to simplify equation i we shall presume that information technology is zilch. This represents the comparative judgment in which the evaluation of one of the specimens has no influence on the evaluation of the other specimen in the paired judgment. The law then takes the post-obit grade.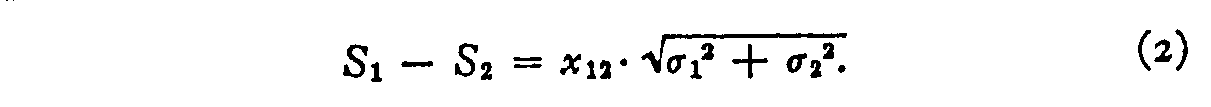

Instance 4.—If we can brand the additional assumption that the discriminal dispersions are non bailiwick to gross variation, we can considerably simplify the equation then that it becomes linear and therefore much easier to handle. In equation (2) nosotros let

σ₂ = σ₁+d,

in which d is causeless to be at to the lowest degree smaller than a _l and preferably a fraction of σ₁ such as .i to .5. And so equation (two) becomes

---

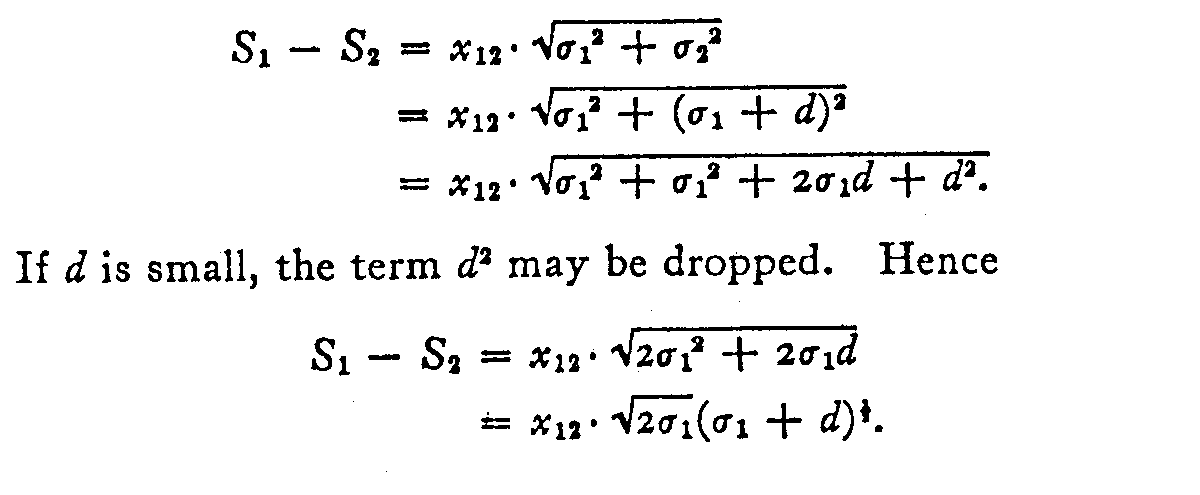
(181)

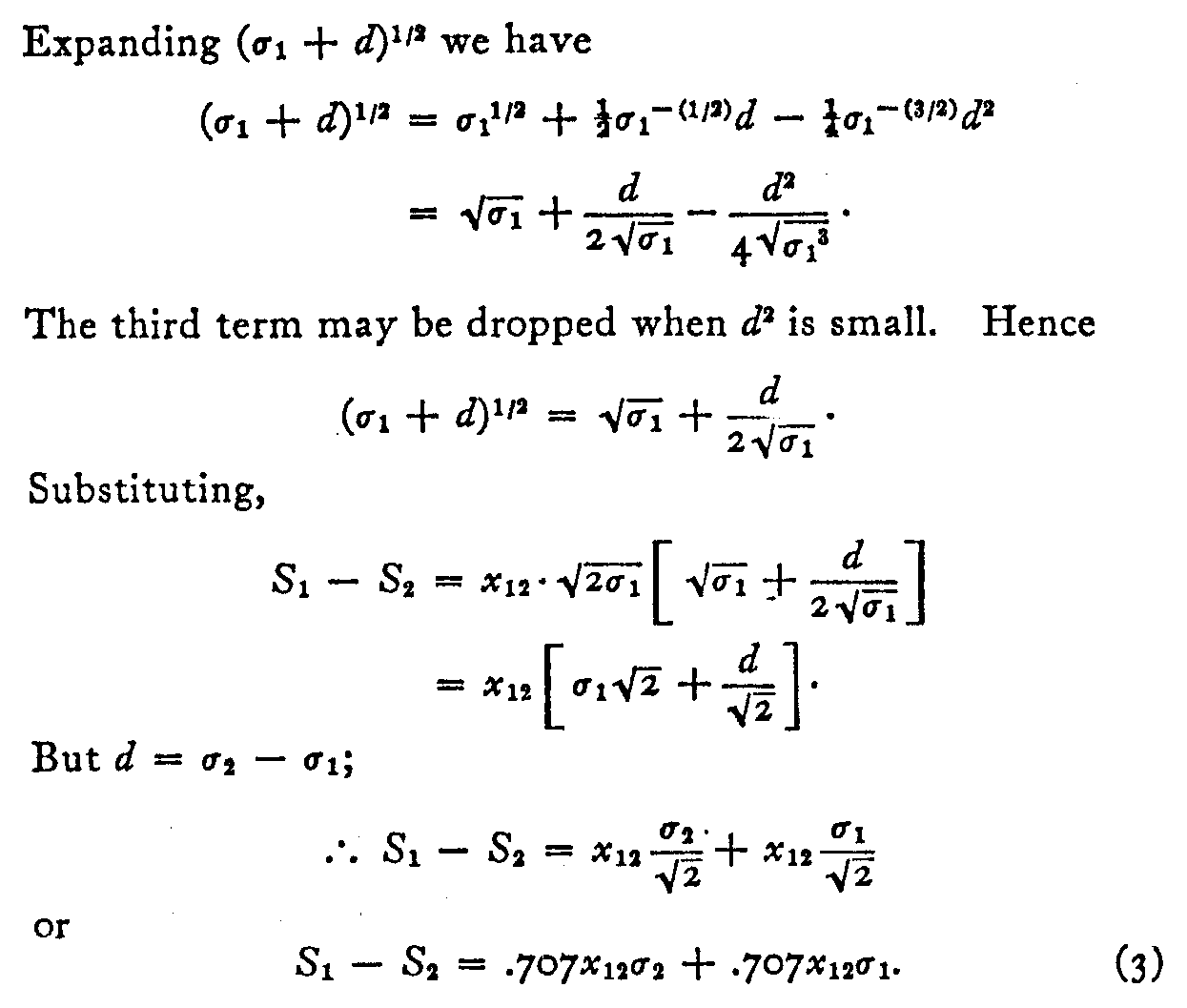
Equation (3) is linear and very easily handled. If σ₂ � σ₁ is minor compared with σ_one , equation (3) gives a close approximation to the true values of S and σ for each specimen.

If there are n stimuli in the calibration there will exist (2n � ii) unknowns, namely a calibration value S and a discriminal dispersion σ for each specimen. The calibration value for 1 of the specimens may be chosen every bit the origin or zero since the origin of the psychological scale is arbitrary. The discriminal dispersion of the aforementioned specimen may be chosen as a unit of measurement for the scale. With northward specimens in the serial there volition exist � n(n � 1) ascertainment equations. The minimum number of specimens for which the scaling problem can be solved is then four, at which number we have six observation equations and vi unknowns.

Case 5.—The simplest case involves the assumption that all the discriminal dispersions are equal. This may exist legitimate for crude measurement such as Thorndike's hand-

---

( 282) -writing scale or the Hillegas scale of English Composition. Equation (two) then becomes

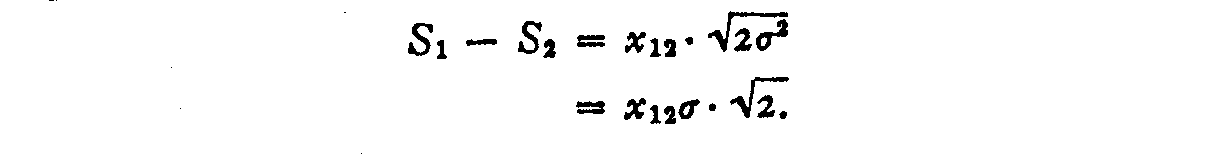
Just since the assumed abiding discriminal dispersion is the unit of measurement we have

Due south₁� S_two = 1.4142x₁₂.(iv)

This is a simple observation equation which may be used for rather coarse scaling. It measures the scale distance betwixt two specimens as straight proportional to the sigma value of the observed proportion of judgments p_l>2. This is the equation that is bones for Thorndike's procedure in scaling handwriting and children's drawings although he has non shown the theory underlying his scaling process. His unit of measurement was the standard difference of the discriminal differences which is .707σ when the discriminal dispersions are constant. In future scaling problems equation (3) will probably be plant to be the almost useful.

WEIGHTING THE OBSERVATION EQUATIONS

The observation equations obtained under any of the five cases are not of the same reliability and hence they should non all be equally weighted. Ii observed proportions of judgments such as p_fifty>2 = .99 and p_l>iii = .55 are not equally reliable. The proportion of judgments p_l>₂ is one of the observations that determine the scale separation between S_fifty and South₂. Information technology measures the scale altitude (S₁— S₂) in terms of the standard departure, σ_1�2, of the distribution of discriminal differences for the two stimuli R_I and R₂. This distribution is necessarily normal by the definition of the psychological scale.

The standard error of a proportion of a normal frequency distribution is

---

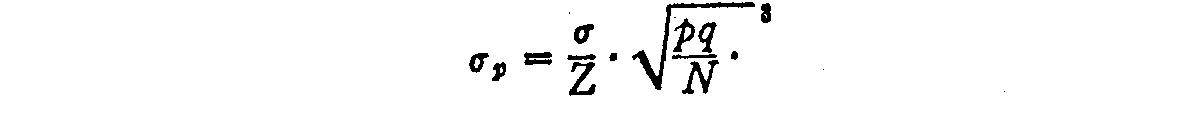
(283) in which a is the standard deviation of the distribution, Z is the ordinate corresponding to p, and q = 1�p while N is the number of cases on which the proportion is ascertained. The term a in the present case is the standard deviation a_fifty—₂ of the distribution of discriminal differences. Hence the standard mistake of p_1>2 is

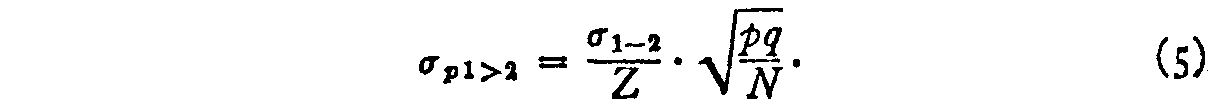
Simply since, past equation (2)

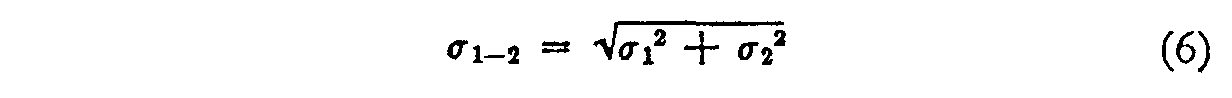
and since this may be written approximately, by equation (3), every bit

σ_i�2 = .707(σ_one + σ₂) (vii)

we take

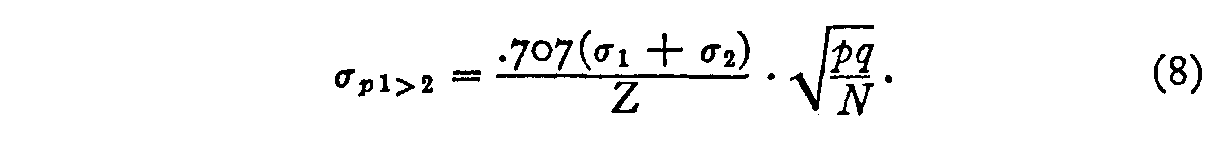
The weight, westward₅₀�_ii, that should exist assigned to observation equation (two) is the reciprocal of the square of its standard error. Hence

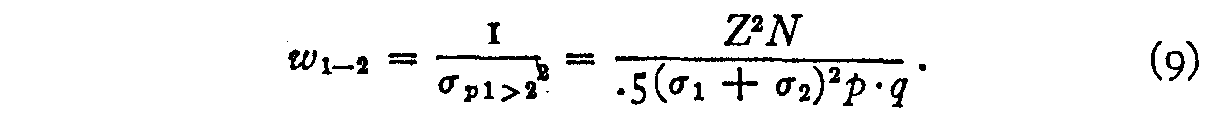
It will not repay the problem to endeavor to carry the factor (σ₅₀ + σ₂)² in the formula because this factor contains two of the unknowns, and considering it destroys the linearity of the observation equation (three), while the only advantage gained would be a refinement in the weighting of the observation equations. Since merely the weighting is here at stake, it may be approximated by eliminating this cistron. The factor .5 is a constant. It has no effect, and the weighting then becomes

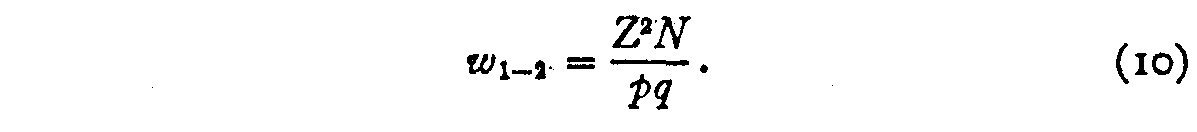
By arranging the experiments in such a style that all the observed proportions are based on the aforementioned number of judgments the factor North becomes a constant and therefore has

---

( 284) no event on the weighting. Hence

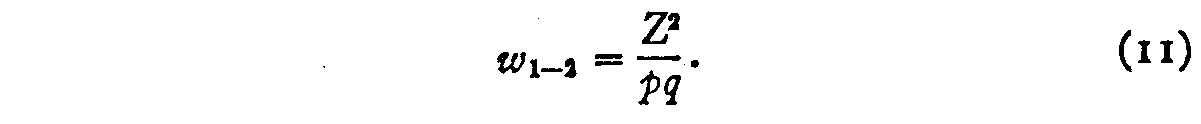
This weighting factor is entirely determined by the proportion, p1>2 of judgments ` I is ameliorate than 2' and it tin can therefore be readily ascertained by the Kelley-Forest tables. The weighted form of ascertainment equation (3) therefore becomes

wS₁ � wS₂ � .707wx₁₂ σ ₂ � .707wx₁₂ σ ₁ = o.(12)

This equation is linear and can therefore be easily handled. The coefficient .707wx₁₂ is entirely determined by the observed value of p for each equation and therefore a facilitating table can be prepared to reduce the labor of setting up the normal equations. The same weighting would be used for any of the observation equations in the v cases since the weight is solely a function of p when a gene is ignored for the weighting formula.

SUMMARY

A constabulary of comparative judgment has been formulated which is expressed in its consummate course as equation (I). This constabulary defines the psychological scale or continuum. It allocates the compared stimuli on the continuum. It expresses the experimentally observed proportion, p_ane>2 of judgments �I is stronger (better, lighter, more excellent) than two ' every bit a part of the scale values of the stimuli, their corresponding discriminal dispersions, and the correlation between the paired discriminal deviations.

The formulation of the law of comparative judgment involves the use of a new psychophysical concept, namely, the discriminal dispersion. Closely related to this concept are those of the discriminal process, the modal discriminal process, the discriminal deviation, the discriminal difference. All of these psychophysical concepts concern the ambivalence or qualitative variation with which one stimulus is perceived by the same observer on different occasions.

The psychological scale has been divers every bit the detail linear spacing of the dislocated stimuli which yields a normal

---

( 285) distribution of the discriminal processes for whatever i of the stimuli. The validity of this definition of the psychological continuum can be experimentally and objectively tested. If the stimuli are and so spaced out on the scale that the distribution of discriminal processes for one of the stimuli is normal, then these calibration allocations should remain the same when they are divers past the distribution of discriminal processes of whatever other stimulus within the confusing range. It is physically impossible for this condition to obtain for several psychological scales defined by different types of distribution of the discriminal processes. Consistency can exist found only for one form of distribution of discriminal processes as a basis for defining the calibration. If, for instance, the scale is divers on the basis of a rectangular distribution of the discriminal processes, it is hands shown by experimental data that there will exist gross discrepancies between experimental and theoretical proportions, p_1>2. The residuals should be investigated to ascertain whether they are a minimum when the normal or Gaussian distribution of discriminal processes is used every bit a basis for defining the psychological scale. Tri-angular and other forms of distribution might be tried. Such an experimental demonstration would institute perhaps the most fundamental discovery that has been made in the field of psychological measurement. Defective such proof and since the Gaussian distribution of discriminal processes yields scale values that agree very closely with the experimental data, I have defined the psychological continuum that is _i-implied in Weber'south Law, in Fechner'southward Constabulary, and in educational quality scales as that particular linear spacing of the stimuli which gives a Gaussian distribution of discriminal processes.

The law of comparative judgment has been considered in this newspaper under five cases which involve different assumptions and degrees of simplification for applied apply. These may be summarized as follows.

Case I.—The police is stated in complete form past equation (I). It is a rational equation for the method of paired comparison. Information technology is applicable to all problems involving the method of abiding stimuli for the measurement of both

---

( 286) quantitative and qualitative stimulus differences. It concerns the repeated judgments of a single observer.

Case II.—The same equation (1) is here used for a grouping of observers, each observer making only one judgment for each pair of stimuli, or one serial ranking of all the stimuli. Information technology assumes that the distribution of the perceived relative values of each stimulus is normal for the group of observers.

Case Three.—The assumptions of Cases I. and 2. are involved here also and in addition it is causeless that the correlation between the discriminal deviations of the aforementioned judgment are uncorrelated. This leads to the simpler course of the law in equation (two).

Instance IV.—Likewise the preceding assumptions the nonetheless simpler form of the law in equation (3) assumes that the discriminal deviations are not grossly unlike so that in full general ane may write

σ₂ — σ_fifty < σ_l

and that preferably

σ₂ — σ₅₀ =d

in which d is a small fraction of σ_l.

Example Five.—This is the simplest formulation of the law and it involves, in improver to previous assumptions, the assumption that all the discriminal dispersions are equal. This assumption should not be made without experimental test. Case V. is identical with Thorndike's method of amalgam quality scales for handwriting and for children's drawings. His unit of measurement is the standard deviation of the distribution of discriminal differences when the discriminal dispersions are causeless to exist equal.

Since the standard error of the observed proportion of judgments, p_1>ii, is non compatible, information technology is advisable to weight each of the observation equations by a factor shown in equation (Two) which is applicable to the ascertainment equations in any of the 5 cases considered. Its application to equation (3) leads to the weighted observation equation (12).

robertstrok1973.blogspot.com

Source: https://brocku.ca/MeadProject/Thurstone/Thurstone_1927f.html

Share this post